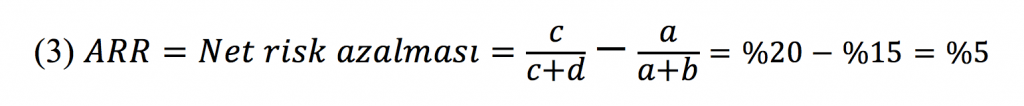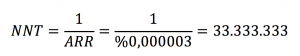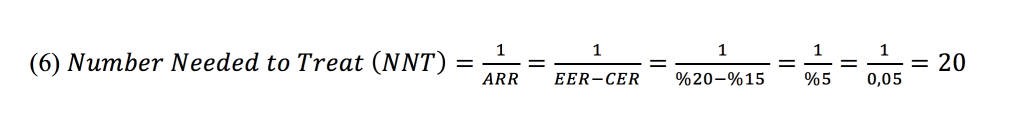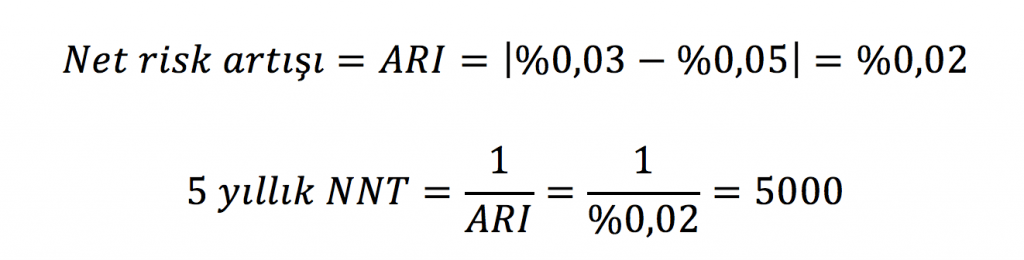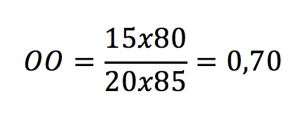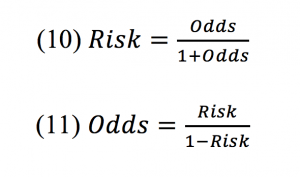Randomize kontrollü bir çalışmada genellikle “evet-hayır” şeklinde dikotom (iki seçenekli) sonlanım ölçütleri değerlendirilir (öldü-yaşıyor, hasta-değil, tanı var-yok). Makalede bu hedef sonlanımın geliştiği ve gelişmediği hastaların hem tedavi hem de kontrol gruplarındaki oranları karşılaştırılır. Bu tip bir sonlanımı bildirmenin olmazsa olmaz şekli 2 x 2 Tablo kullanmaktır.
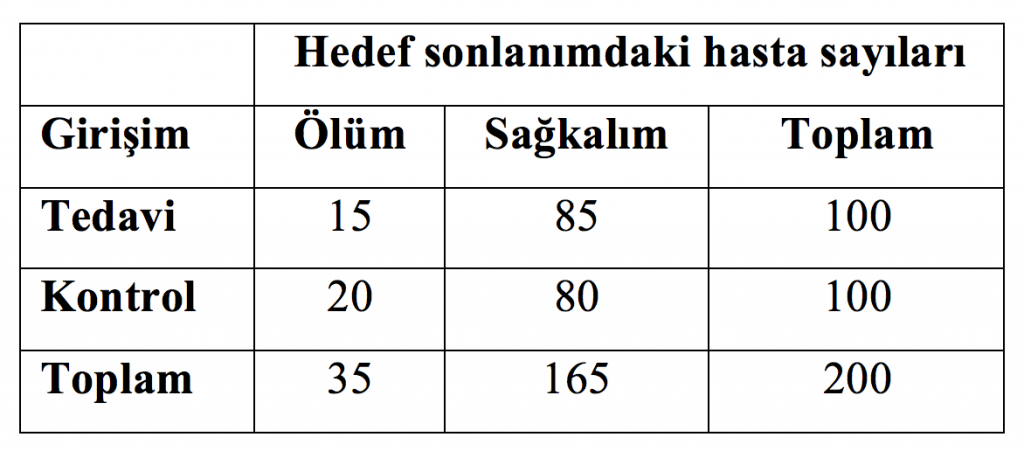
Örneğin, tedavi grubunda hastaların %15’inin, kontrol grubunda ise %20’sinin kötü bir sonlanıma ulaştığı (mesela öldüğü ya da majör bir olayla karşılaştığı) Tablo 1’de 2×2 tablosu verilen bir çalışmayı ele alalım:
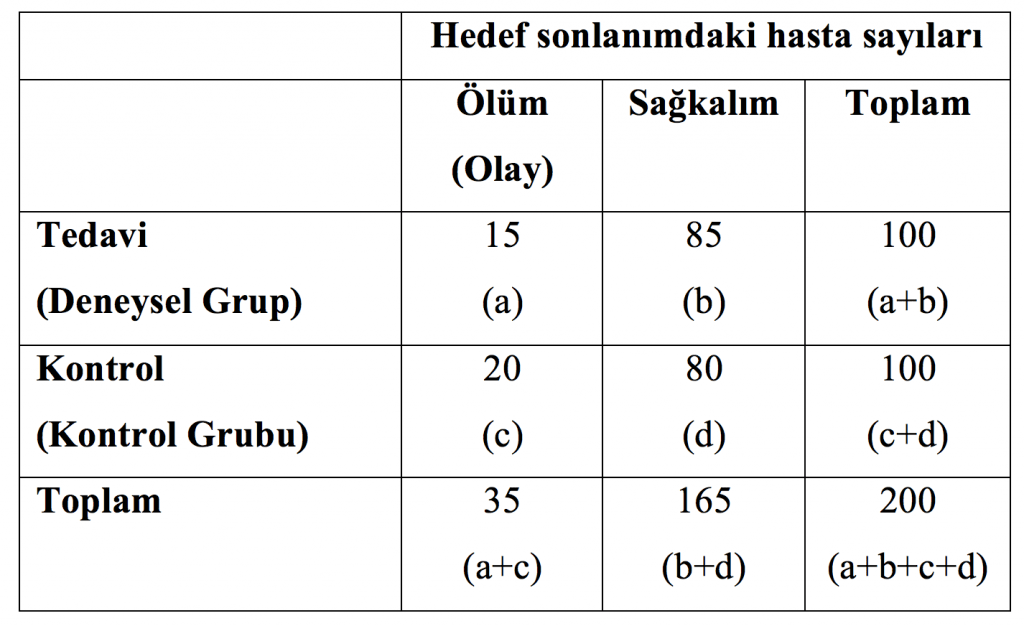
Bu noktada bazı temel terimlerin tanımlamasını yapmamız ve bazı temel hesaplamalar için gerekli formülleri vermemiz gerekli: (Kanıta Dayalı Tıp dili İngilizce olduğundan ve dilimizde bu terimlerin oturmuş bir karşılığı bulunmadığından terimlerin kendimize göre Türkçesinin yanı sıra İngilizce karşılıkları da parantez içinde verilmiştir.) Bu tanımlamaları yaparken Tablo 2’deki kutuların isimlendirmelerinden faydalanacağız.
Tedavi verilen ya da Deneysel grubun tedavi etkisini araştırdığımız sonlanıma (olay, yani burada ölüm) ulaşma oranına deneysel grup riski [Experimental Group Risk = EGR], ya da deneysel olay hızı [Experimental Event Rate = EER] adı verilir.
Kontrol grubunda aynı oran ise kontrol grup riski [Control Group Risk = CGR], ya da kontrol olay hızı [Control Event Rate = CER] olarak adlandırılır ve Formül 1 ve 2’deki şekilde hesaplanırlar.
Bu iki oran arasındaki fark, verdiğimiz deneysel tedavinin kontrol grubundaki ölüm oranını ne kadar azalttığıdır. Örnek üzerinden gidersek, EER %15 (tedavi grubunda 100 hastada 15’i ölmüş) CER %20 (kontrol grubunda da 100 hastadan 20’si ölmüş) iken tedavinin %20 olan ölüm oranını %5 azaltarak %15’e indirdiğini söyleyebiliriz.
İki oran arasındaki net farka net risk azalması [Absolute Risk Reduction = ARR]) adı verilir (Formül 3).
Tedavinin etkinliğini bildirirken kullandığımız bir diğer terim Rölatif Risk ya da Risk Oranı’dır. Deneysel tedavi verilen hastaların ölüm riskinin (EER) kontrol grubundaki hastaların ölüm riskine (CER) oranı olarak ifade edilir. Örneğimize göre,
Yani tedavi grubundaki hastalarda görülen ölüm riski (oranı) kontrol grubunun %75’i kadardır.
Bu tip dikotom sonuçlar bildirilirken en çok kullanılan yol ise rölatif riskin bir başka şekilde ifadesi olan Rölatif Risk Azalması değerinin belirtilmesidir (Relative Risk Reduction = RRR)(Formül 5). Kontrol grubunda olsaydı ölecek olan hastaların %25’i tedavi alırsa ölmeyecektir.
Eğer araştırmacılar Rölatif Riski (RR) belirli bir zaman dilimi için hesaplarlarsa buna da Hazard Oranı (Riziko Oranı) adı verilir.
Çalışmada belirtilmese bile çoğu zaman “X ilacı ölüm riskini azaltmada %30 başarılıydı” ya da “Y tedavisinin etkinliği %80 idi” gibi bir önermeyle aslında Rölatif Risk Azalmasından (RRR) bahsedilir. Eğer deneysel tedavi fayda sağlıyorsa RRR isim değiştirerek rölatif fayda artışı (Relative Benefit Increase = RBI), eğer kontrol grubunda görülen zararı arttırıyorsa rölatif zarar artışı (Relative Risk Increase = RRI) olarak ifade edilir.
Rölatif Risk Azalması (RRR) kullanmanın en önemli dezavantajı tedavi verilmeyen (kontrol grubundaki) hastaların olay riski (CER) hakkında hiçbir bilgi vermemesidir. Bu sebeple de çok küçük riskler olsa bile aralarındaki oransal farkı ifade etmesi yüzünden etki çok büyük gibi görünebilir. Örneğin, %0,000012 olan ölüm riski tedavi ile %0,000009’a düşüyorsa aslında tedavinin sağladığı net risk azalması sadece %0,000003 iken rölatif risk azalması %25’dir. Bu gibi durumlarda net risk azalmasının (ARR) ifade edilmesi çok daha doğrudur. Bu tip önermeleri farmasötik şirketlerinin hekimlere tanıtımda kullandığı materyallerde sıklıkla görebilirsiniz.
Bu ifadelerin elle tutulur bir gerçeğe dönüştürülmesi ihtiyacıyla tedavi edilmesi gereken sayı (Number Needed to Treat (NNT)) terimi tanımlanmıştır (Formül 6). Net risk azalmasının tersi olan bu tam sayı gündelik pratikte algılanabilir bir ölçektir. Çalışmadan belirtilen tedavi süresi boyunca gelişebilecek kötü sonlanım sayısını (olay, ölüm vb.) 1 tane azaltabilmek için kaç hastaya deneysel tedavinin uygulanması gerektiğini gösterir. Bir önceki paragrafta yer alan örnekten devam edersek ARR %0,000003 olduğuna göre
olarak hesaplanabilir. Bu sayı, tedavi verilmediği takdirde ölecek olan 1 hastanın yaşayabilmesi için 33 milyon hastaya tedavi verilmelidir anlamına gelir! 1 hastada tedavi faydası görebilmek için milyonda 1 görülecek bir yan etkiden 33 kişinin zarar görecek olmasının mantıklı olmadığını rahatlıkla söyleyebiliriz. Halbuki, RRR (rölatif risk azalması) %25 gibi gayet anlamlı bir tedaviden bahsetmekteydik. Genel olarak, NNT ne kadar küçükse tedavinin etkisi o kadar güçlü, ne kadar yüksekse o kadar düşüktür.
Yan etki için de aynı mantıkla advers bir olay görülmesi için tedavi edilmesi gereken hasta sayısı (Number Needed to Harm (NNH)) hesaplanabilir. Bu hesaplamada net risk artışı (ARI) kullanılır. Beş yıl boyunca tedavi etkisinin izlendiği bir statin çalışmasında kontrol grubunda %0,03 rabdomiyoliz görülürken bu oran tedavi grubunda %0,05 olarak gözlenmiş olsun.
Tedavi verilen hastalarda kontrol grubuna göre fazladan 1 kişide daha rabdomiyoliz görülmesi için 5000 hastaya 5 yıl boyunca statin verilmesi gereklidir.
Çalışmaların bazılarında yazarlar riskleri vermeyi tercih ederken diğerlerinde Odds Oranının (OR = OO) kullanıldığını göreceksiniz. Bu tercih kişisel bir tercih olup aslında aynı şeyleri ifade eden sayıların farklı gösterim şekillerinden ibarettir. Odds terimi özellikle ülkemizde herkesin kafasını karıştıran bir terim. Aslında bu terim İngiliz kumar ve bahis jargonundan gelir ve olasılık istatistiklerine de aynı kelimeyle geçmiştir.
Rulet oyunu üzerinden örnek verirsek, kırmızı ya da siyah gibi 2’li bahislerden birine oynayıp kazandığınız takdirde yatırdığınız her 1 birim karşılığında 1 birim daha kazanırsınız. İlk başta koyduğunuz kendi bahsinizi kaybetmediğiniz için paranız 2 katına çıkar. Bu bahsin oddsu 1’e 1, 1:1 ya da 1’dir. “Kaybedersen 1 birim kaybedersin ama kazanırsan 1 birim daha kazanırsın”, ya da her “1 birim kazancın için ben 1 birim kaybederim” şeklinde de ifade edilebilir. Rulette herhangi bir sayıya oynadığınız takdirde risk ettiğiniz ve kaybedebileceğiniz her 1 birim için 35 birim kazanırsınız, yani 1’e 35 kazanırsınız, ya da odds 1:35 veya 35’dir. Kazandığınız takdirde elinizdeki para yatırdığınız da dahil olmak üzere ilk bahsinizin 36 katıdır.
Bir başka örnek ile tekrarlayalım: 6 yüzlü bir zar attığınızda, tuttuğunuz sayının gelme olasılığı (ihtimali) 6’da 1 yani 1/6, gelmeme ihtimali de 6’da 5 yani 5/6’dır. Tuttuğunuz sayının gelme olasılığının (ihtimalinin), gelmeme olasılığına oranı olan 1:5 olup odds 1:5 ya da 5’dir. Bunu, “tuttuğunuz zarın gelme ihtimali 1’e 5’tir” olarak da söyleyebiliriz (6’da 1 ve 1’e 5 aynı şansın farklı sayısal gösterimleri: ilki olasılık, ikincisi odds).
Peki, zar atımında tek sayı gelme oddsu nedir? 6 sayıdan 3’ü tek 3’ü çift olduğuna göre 3:3 ya da 3’e 3’tür. Bu da 1 oddsa karşılık gelir (3:3 = 1:1). Yani, tuttuğunuz sayının (bu örnekte tek sayılar) gelme olasılığı, gelmeme olasılığına (çift sayılar) denk olduğundan odds 1’dir. Bu söylem istatistik bilimine geçerken biraz erozyona uğrar ve kaybedeceğin:kazanacağın oranı olan odds, olma olasılığı/olmama olasılığı, ölüm/sağkalım, sağlıklı/hasta haline dönüşür.
Dört gözlü tablodaki örneğimize dönelim: Tedavi grubunda 15 kişi ölürken 85 kişi yaşamıştır (Formül 7). Yani tedavi grubunda ölüm oddsu 15:85 ya da 3:17’dir. Ölen her 3 kişiye karşılık 17 kişi yaşamış, 20 kişiden 3’ü ölmüş veya 20 kişiden 17’si yaşamıştır. Kontrol grubunda ölüm oddsu 20:80 veya 1:4’tür (Formül 8). Ölen her 1 kişiye karşılık 4 kişi yaşamış, 5 kişiden 1’ü ölmüş veya 5 kişiden 4’ü yaşamıştır. Tedavi ve kontrol gruplarının oddsları arasındaki orana ise Odds Oranı ya da tam ifadesi olmamakla beraber Olasılıklar Oranlarının Oranı (Odds Oranı, OO) adı verilir (aslında olasılıklar oranı sizin de gördüğünüz gibi oddsun kendisi. Dolayısıyla odds oranına da olasılıklar oranlarının oranı dememiz lazım. İşte odds oranında kafa karışıklığının sebebi buradan geliyor). Tedavi grubunun ölüm oddsunun kontrol grubun ölüm oddsuna oranı olan odds oranı,
olarak hesaplanabilir (Formül 9). Eğer odds oranı 1 ise tedavinin kontrol grubuna göre farklı bir olasılığa sahip olmadığını söyleyebiliriz. Eğer odds oranı 1’in üstündeyse odds oranına bakılan olay ya da sonlanım tedavi ile artmakta, altındaysa azalmaktadır.
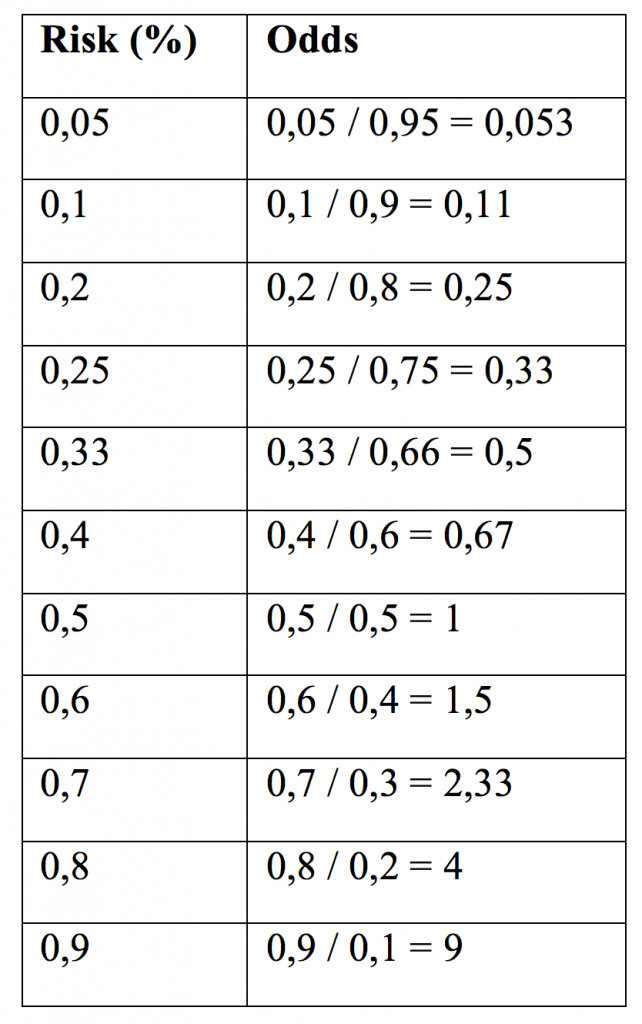
Hangi Odds’un hangi Riske karşılık geldiği Tablo 3’de gösterilmiştir. Odds ve Riskin birbirine dönüşüm formülleri Formül 10 ve 11’de verilmiştir.
Odds’lar görüldüğü gibi daima risklerden sayısal olarak daha yüksektir. Risk çok yüksekse odds ve risk arasındaki fark daha da büyür, risk çok düşükse arada neredeyse hiç fark kalmaz. Klinisyenler olarak anlaması ve algılaması çok daha kolay olan RR’nin OR’yle ilişkisini bilmek ve her ikisini birbirine dönüştürebilmek durumundayız. Şansımıza, tıbbi uygulamalarda hastalarımızın karşı karşıya kaldığı riskler genellikle düşük olduğundan RR ve OR birbirine yakındır. OR kullanıldığında tedavinin sanki daha etkinmiş gibi bir algılaması oluşur.
Örneğin, bir ilacın etkinliği (istenen sonuç) tedavi grubunda %45 kontrol grubunda %30 ise, tedavi grubunun oddsu 0,82 (0,45 / 0,55) iken kontrol grubunun oddsu 0,43 (0,30 / 0,70) olup, RR 1,5 (0,45 / 0,30) OR 1,91’dir (0,82 / 0,43).
Peki, madem OO işleri bu derecede karıştırıyor ve anlaması da zor, neden kullanmaya devam ediyoruz? OO yukarıda bahsettiğimiz örneklerdeki randomize kontrollü çalışmalardan ziyade gözlemsel kohort çalışmalarda daha faydalıdır. Kohort çalışamalarda, araştırmacılar belirli risklere sahip hastaları belirli bir zaman izler ve oluşan istenmeyen olayların frekanslarının kaydını tutar. Vaka-kontrol çalışmalarında ise katılımcılar halihazırda zaten istenmeyen sonuca ulaşmıştır. Araştırmacılar bu sonlanıma ulaşmış hastalara denk bir kontrol grubu seçer (bu kontrol grubunda kaç kişi olacağına ve vakalarla oranına çalışmacılar karar verir) ve geriye dönük olarak her iki grubun geçmişinde risk varlığının oranını karşılaştırır. Bu tip çalışmalar hastalıkların prevalansı hakkında bilgi vermez, çünkü hasta ve kontrol sayısı hastalığın toplumdaki prevalansına denk şekilde değildir, araştırmacıların tercihleriyle oluşturulmuştur.
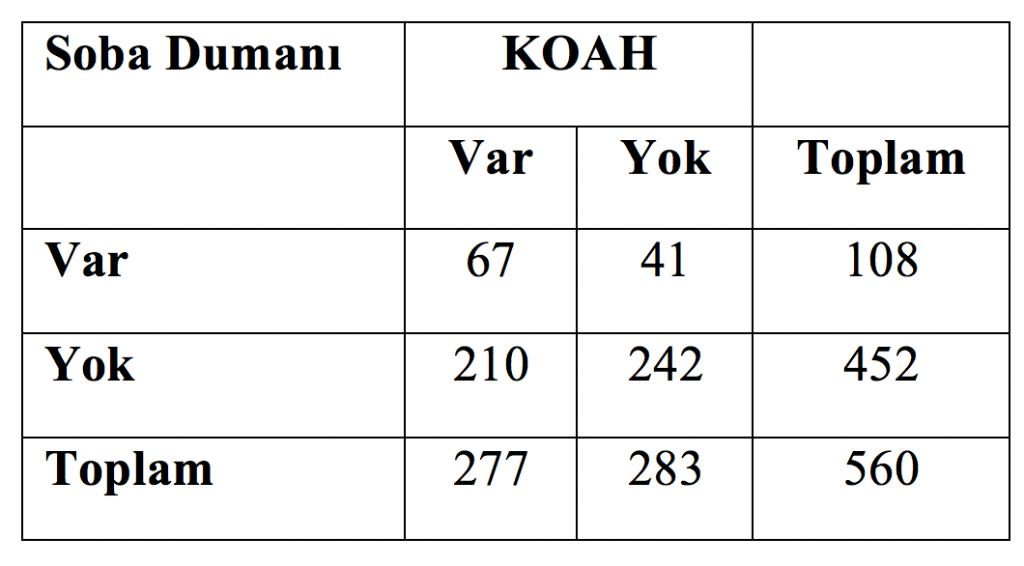
Örneğin, KOAH gelişiminde en az 1 yıl soba bulunan bir evde yaşamanın etkisi bir vaka-kontrol çalışmasıyla incelenmek istense, KOAH hastası olan bir grup ile kendi seçeceğimiz bu gruba denk bir kontrol grubunun özgeçmişlerindeki sobalı evde yaşama durumlarının frekanslarını karşılaştırmamız gerekir. 277 KOAH hastamız olduğunu ve bunların 67’sinde soba dumanı maruziyeti olduğunu varsayalım. Kontrol grubu olarak da KOAH dışındaki değişkenler açısından bu gruba denk, polikliniğimize başvuran 283 hasta seçmiş olalım ve bunların da 41’inde soba maruziyeti belirlemiş olalım. Bu durumda örneğimizin dört gözlü tablo yapısı Tablo 4’deki gibi olacaktır.
Bu tablodan yola çıkarak;
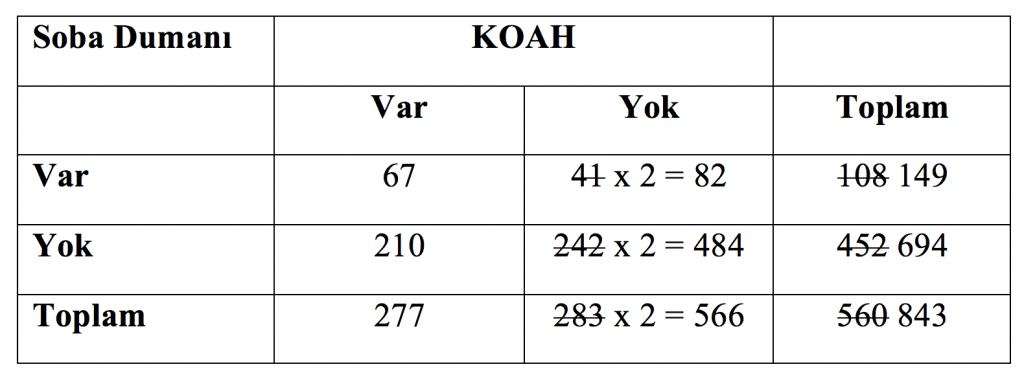
risk nispeten orta seviyede olduğundan RR ile OO arasında fark olduğunu, OO’nun daha yüksek olduğunu görürüz. Araştırmacılar tam 2 katı büyüklükte bir kontrol grubu seçseydi sonuçlarımız değişir miydi? (Tablo 5)
Bu durumda,
Görüldüğü gibi, vaka-kontrol çalışmalarında rölatif risk tamamen kontrol grubundaki hasta sayısına bağlı iken, odds oranı kontrol grubunun hasta sayısı ile değişmemekte.
Bu sebeple, odds oranı vaka-kontrol çalışmalarında kullanılması ve raporlanması gereken ölçüttür.
OR’nin diğer önemli özellikleri ise şunlardır:
- Meta-analizlerde birbirinden çok farklı olay oranları bir araya getirilmeye çalışıldığından aynı mantıkla RR yerine OO kullanılması gerekir.
- OO, maruziyete bağlı birbirini tamamlayan sonlanımınların yönüne göre birbirinin tersi değerler alır. Mortalite için bakılan OO 4 ise, sağkalım için aynı çalışmada OO ¼’tür.
- Risk ne kadar büyürse büyüsün RR tam anlamıyla yükselmez. Halbuki OO temel risk oranının büyüklüğünden etkilenmez. OO, 0 ile sonsuz arasında değerler alabilirken, RR alamaz.
- OO, maruziyet ile sonlanım arasındaki ilişki ve etkinin büyüklüğünün ölçüsü olduğundan lojistik regresyon için kullanılan parametredir. Tarihsel açıdan OO her türlü ilişki bildirimi için tercih edilen ve daha doğru kabul edilen ölçüt olsa da modern istatistiksel yöntemler kullanıldıkça önemliliği azalmaktadır.