1920’lerde Fisher p degeri’ni tanımladığında birgün bu kadar yanlış anlaşılacağını bilseydi herhalde matematiği bırakıp inzivaya çekilirdi. P değeri ve anlamı günümüzde akademik dünyanın açık ara ile en büyük ve en yaygın yanlış anlaşılmasıdır. Bu yanlış anlaşılma hatta anlaşılamama durumunu bir nebze hafifletmek amacıyla hayali bir çalışma kurguladım. Sizlerle beraber bu çalışmanın verileri üzerinde oynayarak p değeri ve güven aralıklarının gerçek hayatta neler ifade ettiğini anlamaya çalışacağız. Anlaşılmaz istatistiksel kavramlardan uzak durmaya gayret etsem de çok başarılı olamadığım yerler de oldu. Bu açığı deva eden yazılarla kapatmaya çalışacağız. Eğer yarım saatinizi vermeye hazırsanız, başlayalım…
İlk çalışma: bir erkeğin anatomisi

Bir grup araştırmacı, erkek asistanların kadın asistanlar tarafından beğenilmelerinde yeni trend olan sakal bırakmanın etkisini incelemek üzere bir araştırma planlarlar (konu üzerinde fazla düşünmeme gerek kalmadı, çünkü tüm asistanların birden 2 karış sakalla gezmeye başlamasında 20’li yaş grubu için ilk hipotez daima karşı cinsle ilgili olmak durumundadır. Mesela durduk yere nöbet değişmek, rotasyona çıkmak için aşırı heveslenmek, nöbeti yokken hastanede görünmek gibi). Farklı hastanelerde farklı ihtisas dallarında asistanlık yapan erkekler yaş, boy, kilo gibi faktörler açısından stratifiye edilmiş gruplar içine kurumlar ve ihtisas dalları arasında fark olmayacak şekilde örneklendikten sonra (226 erkek asistan) sakal bırakan (n=112) ve her gün tıraş olan (n=114) gruplarına randomize edilirler (dolayısıyla “sakal bana yakışıyor abi” diyenlerle eskikız arkadaşı beğendi diye bırakıp sonra vazgeçemeyenlerden kaynaklanan biası minimize etmeye çalışıyoruz). Sıfır hipotezimiz sakallılar ile sinekkaydılar arasında fark olmadığı, alternatif hipotezimiz ise birinin daha çekici olduğu şeklinde. Çalışmanın birincil sonlanım noktası (hedefimiz) aynı şekilde örneklenmiş kadın asistanlar tarafından 10 üzerinden bu erkek asistanların çekiciliklerinin puanlanması, toplu ortalamalarının alınması ve her erkek asistanın buna göre çekici ya da değil olarak sınıflandırılması sonrasında sakal grupları arasındaki farkın incelenmesidir (bu değerlendirme elbette subjektif bir ölçümün kantitatif veriye dönüştürülmesi olduğundan kendi içinde yanılgı payı var. Ancak sosyologlar çekiciliğin aslında subjektif olmadığını, çekici olan kişiler üzerinde herkesin hemfikir olduğunu, eğer hemfikir değillerse o kişinin çekici olmadığını belirten çalışmalar yapmışlar). Sonuç olarak her gün tıraş olan asistanlar içerisinde çekici olarak tanımlananların sayısı daha fazla olsa da aradaki fark istatistiksel olarak anlamlı bulunmamıştır (sakal bırakanlar: 33/112 (%29,4) – tıraş olanlar: 41/114 (%35,9); P=0,32) (Burada da aslında bir bias var, çekici olan sakal bıraksa da bırakmasa da çekicidir. Ama zaten bu sebeple grupları randomize ettik, iki gruba da eşit sayıda Brad Pitt düşsün diye).
Buradaki p değerini aşağıdakilerden hangisi en iyi tanımlar?
a) Sıfır hipotezinin (sakal makal farketmez, önce bakarım adam mı diye) doğru olma olasılığıdır.
b) Alternatif hipotezin doğru olma olasılığıdır.
c) Araştırma yapılan gruplar arasında fark olmadığı sürece sonlanım ölçütünde gözlenen fark (%35,9-%29,4=%6,5) ya da daha fazlasını elde etme ihtimalidir.
d) Gözlenen fark (%6,5) ya da daha fazlasının şans eseri olma ihtimalidir.
[toggle title=”Cevap için tıklayın” state=”close”]En iyi yanıt C seçeneğidir.[/toggle]
Çalışmanın sıfır hipotezi örneklemin alındığı erkek asistanlar popülasyonunda sakal bırakan ya da her gün tıraş olan erkek asistanlar içinde, kadın asistanların puanlamasında çekici olarak belirlenen erkek asistan oranı açısından fark olmadığıdır (sakal makal farketmez). Alternatif hipotez ise iki yönlüdür. Ya sakal bırakanlarda ya da her gün tıraş olanlarda çekici olarak belirlenen erkek asistan oranı daha fazladır.
P değeri, sakal bırakan ve her gün tıraş olan erkek asistan gruplarında kadın asistanlar tarafından çekici olarak tanımlanan asistan oranları arasında gözlenen en az %6,5’lik farkın, aslında hiç fark olmamasına rağmen görülebilme ihtimalidir. Yani bu sayıda asistan kullandığımda %32 ihtimalle arada fark olmamasına rağmen en az %6,5 fark varmış gibi sonuç alabileceğimizi belirtir. Ki-kare testi kullanarak bulduğumuz p değeri tam olarak bu olasılığı ifade eder.
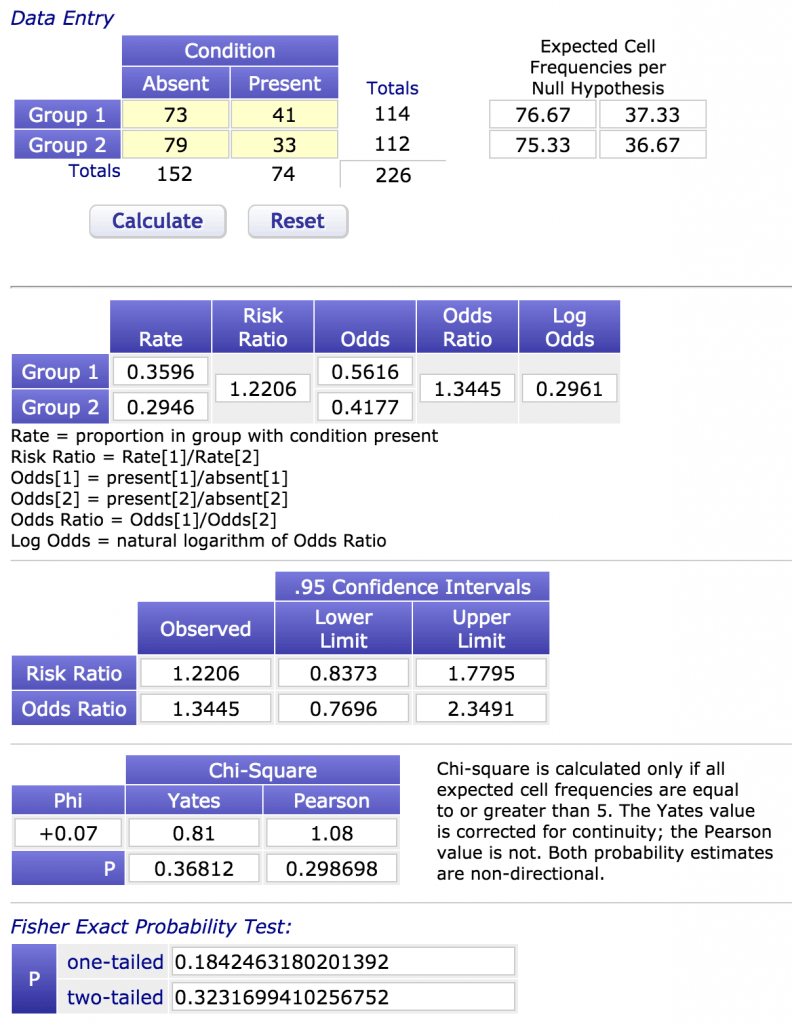
Verilerimizi hesaplama sitesinde yerlerine koyduk ve aşağıda yer alan ilk hesap tablosunu oluşturduk. Bu hesap tablosunun biraz ayrıntısına inelim: Her gün tıraş olanların 41 tanesi çekici iken (%35,9) sakal bırakanların 33’ü çekicidir (%29,4). Yani çekici olanların sayısı her gün tıraş olanlarda 1,22 kat (%35,9/29,4) daha fazladır. Her gün tıraş olan asistanların çekici olma odds’u (çekici olanların olmayanlara oranı) 0,56; sakal bırakanların çekici olma odds’u 0,41’dir. Bu iki odds arasındaki orana odds oranı denilir ve 1,34’dür (0,56/0,46). Bu ise her gün tıraş olanların çekici olma olasılığının sakallı gezenlerin çekici olma olasılığının 1,34 katı (ya da %34 daha fazla) olduğunu gösterir. Bu değerin hemen beraberinde bir de %95 güven aralığı gelir genellikle (otomatik olarak yazılım hesaplar bunu). %95 güven aralığı, eğer biz aynı kıstasları kullanarak aynı asistan evreninden 20 örneklem seçseydik 19’unda elde edeceğimiz sonuçların yer alacağı aralığın üst ve alt sınırlarıdır (95/100=19/20). Aynı veriye göre 20 farklı erkek asistan grubunu değerlendirirsek 19’unda çekici olma olasılıkları oranı 0,77 ile 2,35 kat arasında iken, 1’inde bu aralığın dışındadır (ilk tabloya bakalım). Yani 20’de 19 ihtimalle sinekkaydıların 1,34 kat olan çekici olma olasılık oranı, farklı bir örneklem alınırsa 2,35 kat’a çıkabilirken, tam tersine bir başka grupta sakalla gezenlerin çekici olma olasılığı 1,29 kat daha fazla çıkabilir (0,77 – 100/77=1,29). Sonuç olarak, elde ettiğimiz veriye göre sakallılar ya da sinekkaydılar daha fazla çekici olma olasılığına sahip demek mümkün değildir (matematiksel olarak odds oranının %95 güven aralığı içinde 1 yer alır, ya da sınırlardan biri 1’den küçükken diğeri büyüktür, yani oranlarının 1 olma ihtimali söz konusudur). Çalışma sonunda sakal kesmek ya da kesmemenin erkek asistanların çekiciliğine bir katkı sağlamadığı, önemli olanın iç güzellikleri oldukları yorumu yapılarak çalışma yayınlanır, çalışmaya istinaden de herkesin sakallarını kesmesi istenir.
Big Shave: Şeytani tıraş makinasi firma çalışması
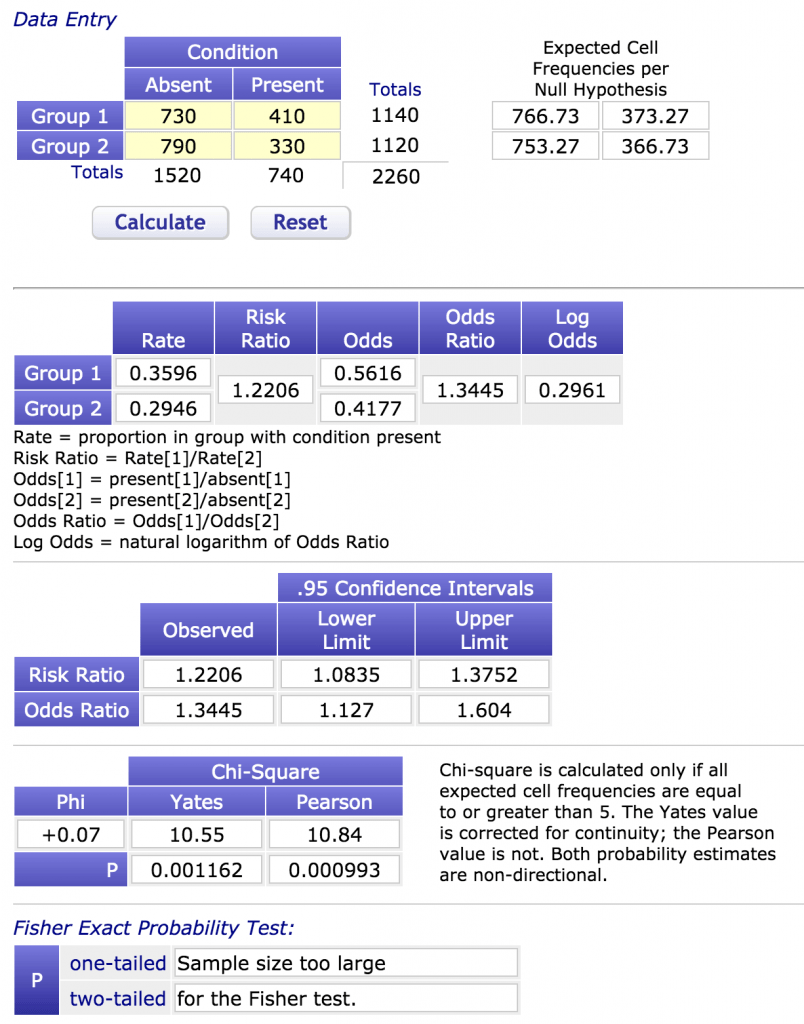
Ardından bir tıraş makinesi firması az buz erkek asistan olmadığı, iş-güç yüzünden 30’lu yaşlarına kadar bekar gezdikleri ve eğer erkek asistanların tıraş olduklarında daha çekici oldukları yönünde güçlü bir veri sağlayabilirse makine satışlarını patlatabileceği yargısına varır. A cihazıyla tıraş olmak (girişim-intervention) ya da tıraş olmamak (kontrol) gruplarına tamamen aynı demografik oranlarla erkek asistanları randomize ederler. Ama yatırım güçleri daha fazla olduğundan 226 erkek asistan değil de 2260 erkek asistanı çalışmaya alırlar. Şansa bakın ki çalışmanın tüm verileri birebir aynı çıkar. Aradaki fark yine %6,5’dir. Çekici olanların olmayanlara oranı (odds) ve tıraş olanlarla olmayanların çekici olma olasılıklarının oranı (odds oranı) da doğal olarak birebir aynıdır. Ancak bu sefer güven aralığı çok daha dardır. 20 farklı 2260 kişilik örneklemler alsaydım 19’unda çekici olma olasılıkları oranı 1,13 ile 1,60 kat arasında değişecek, ancak 1 seferinde ise bu aralığında da dışında olabilecekti (%95 güven aralığı, %5 ihtimalle yanılacağım anlamına gelir). Yani 20 seferin 19’unda öyle ya da böyle sinekkaydı ekibin içinde yer alan bir asistanın çekici olma olasılığı daha fazla diyebiliriz. Bu 20’de 1 tamamen yanılma durumuna (ki biz bu miktarda yanılmayı kabulleniyor ve %95 güven aralığı seçiyoruz başta, örnekleme hatası da denir. Eğer %5 size fazla geliyorsa %1 (%99 güven aralığı) yanılma payı da bırakabilirsiniz, ancak o zaman daha geniş bir aralık bulacaksınız). Hesapladığımız bir diğer değer ise P değeri olup 0,0012’dir. Aynı sayıda asistan kullandığımda arada fark olmamasına rağmen %0,12 ihtimalle en az %6,5 fark varmış gibi sonuç alabileceğimizi belirtir. Arada fark yokken hata yapıp en az %6,5 fark varmış gibi bulma ihtimalimiz neredeyse yoktur. Arada bulduğumuz farkın gerçekliğine güvenebileceğimiz anlamına gelir. Bu hesaplamayı da aşağıdaki tabloda görebilirsiniz.
Örneklemimiz küçük olduğundan fark bulamadık, biri paraya kıyıp daha geniş örneklem ile anlamlı fark bulacak ama fikir benden çıktı çalışması
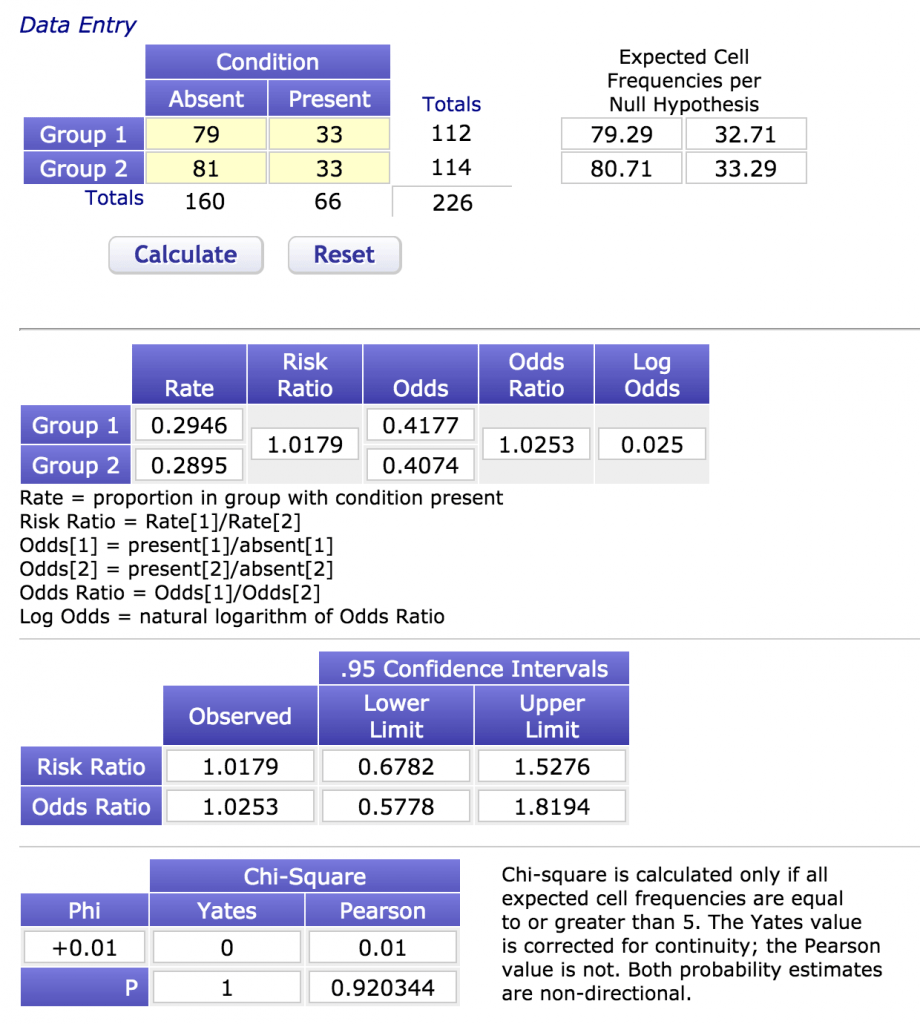
Şimdi işleri biraz karıştıralım. Çekici olarak tespit edilen asistan oranları şu şekilde olmuş olsun: sakal bırakanlar: 33/112 (%29,4) – tıraş olanlar: 33/114 (%28,9). Yani her iki grupta da aynı sayıda çekici asistanımız var ve oranlar da neredeyse aynı. P değerini hesapladığımızda tam 1 olduğunu görüyoruz (Yine aşağıdaki tablodan takip edelim). Peki bu ne demekti? Aynı sayıda asistan kullandığımda arada fark olmamasına rağmen %100 ihtimalle en az %0,5 fark varmış gibi sonuç alacağız demek (%29,4-%28,9=%0,5). Odds oranı 1,02 %95 güven aralığı ise 0,58 ile 1,82 arasında. Bu sonuç ise aynı sayıda asistan içeren tıpatıp benzer ama farklı 20 örneklem alsam 19’unda bir grubun diğerinden daha çekici olma miktarının yüzdesel olarak büyüklüğünün ters yönlerde %82 ile %72 (100/58) arasında değişebileceğini gösteriyor (1,82 odds birinin diğerine göre çekici olma olasılığının %82 daha fazla olması demek, 0,58 ise tam tersine az olması. 58 sayısı 100’den %42 daha azdır, ama 100 sayısı 58’den %72 daha fazladır. Tamamen akıl karıştırıcı matematik.). P değeri arada bulduğum farka güvenmemem gerektiğini belirtirken, odds oranı ise bu farkın anlamlılığını düşünmemi sağlıyor.
RAZ-R: Biggest Shave Çalışması: Çok merkezli, 10 yıllık çalışma. Artık gönül rahatlığıyla hepimiz tıraş makinası alabiliriz
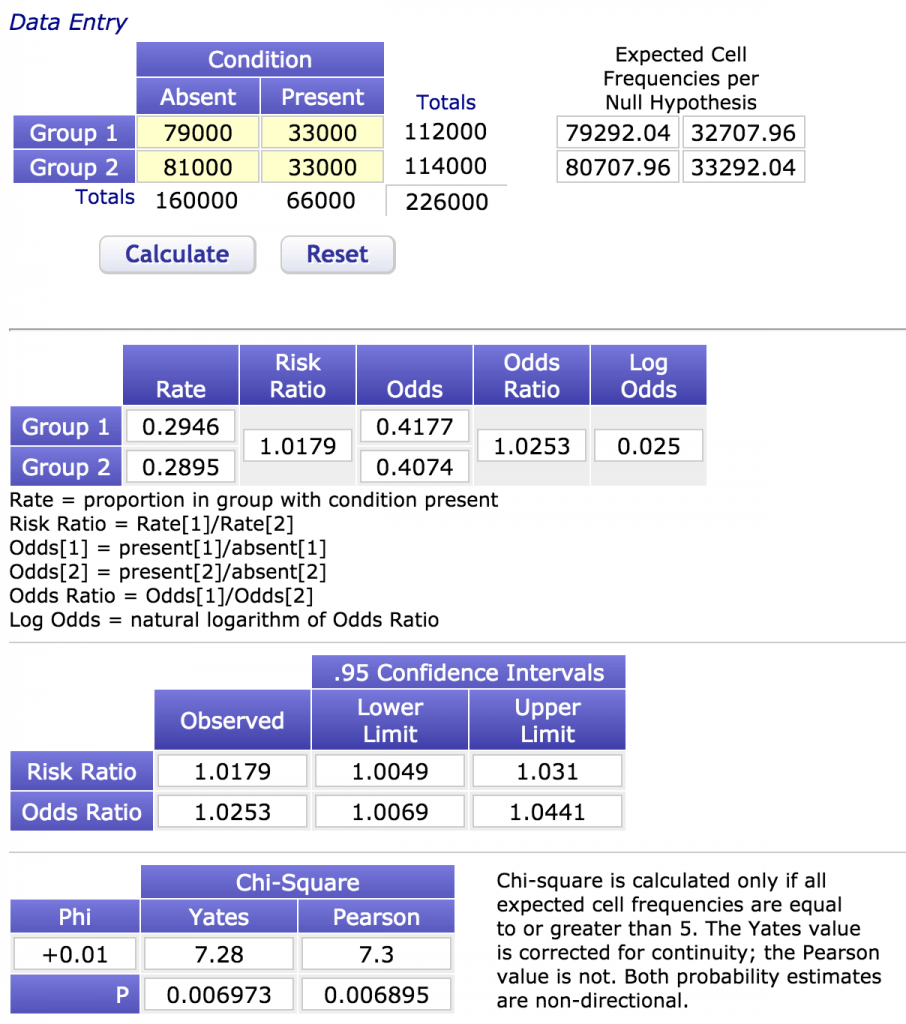
Yine tıraş makinası firmasının yaptığı bir hit çalışma sayesinde işler biraz daha karışıyor. Bu sefer o kadar azimliler ki birçok ülkede birçok asistanı çalışmaya alıyor ve dünya çapında birkaç yıl süren bir çalışma yapılmasına ön ayak oluyorlar. Sonuçta tam 226000 asistanlık dev bir çalışma elde ediliyor (ilk çalışmamızın tam 1000 katı). 33000/112000 (%29,4) – tıraş olanlar: 33000/114000 (%28,9). P değeri tam 0,006973! Aynı sayıda asistan kullandığımda arada fark olmamasına rağmen sadece %0,6 ihtimalle en az %0,5 fark varmış gibi sonuç alabileceğimiz görülüyor. Verilerimiz çok keskin, aradaki farkı çok büyük ihtimalle doğru olarak tespit etmiş durumdayız. Peki ama esas önemli soruyu atlamayalım. Fark ne kadar? Sinekkaydı tıraş olan asistanlar, sakalla gezenlerden çekici olma olasılığı açısından tam 1,02 kat daha şanslı ve bu üstünlük istatistiksel olarak da 20 farklı örneklemin 19’unda geçerli! Güven aralığı da oldukça dar, olsa olsa bu odds oranı 1,0069 kat ile 1,0441 arasında değişebilir. Peki bu ne demek? Son derece anlamlı bir şekilde %0,69 ile %4 arasında değişen miktarda çekici olma ihtimaliniz var demek. İlk çalışmada %6,5 farkı bile anlamlı bulmazken şimdi %0,69 kadar az bir farkı anlamlı bulup buna göre karar vermek demek. Haydi hep beraber tıraş makinası almaya… (mı acaba?)
Düşman kardeşler: Fisher, Neyman ve Pearson
Yukarıda ironi ve abartı ile verdiğimiz 4 örnek sanırım bir noktaya açıklık getirmiştir. P değerinin baktığımız karşılaştırmanın anlamlı olup olmamasıyla ilgili bir söyleyeceği yoktur. P değeri bulduğunuz farkın rastlantısal olarak gerçekleşme olasılığını size belirtir. Teorik olarak belirlenen p=0.05 sınırı, fark olmamasına rağmen örneklemimizin fark varlığını göstermesini (örnekleme hatası) %5 ihtimali aşmadığı sürece makul karşıladığımız anlamına gelir. Tip I hata olarak da tanımlanır (her ne kadar tip I hata her zaman örnekleme hatasına eşit olmasa da şimdilik genel kanıyı kabul edelim).
Ronald Fisher 1920’ler p değerini ilk ortaya attığında bunun definitif bir test olarak algılanacağını hiç düşünmemişti. 20’lerin sonunda, Fisher’in en azılı rakipleri olan Polonyalı matematikçi Jerzy Neyman ve İngiliz istatistikçi Egon Pearson, veri analizi için güç (power), yanlış pozitif, yanlış negatif ve diğer konseptleri ortaya atıp özellikle p değerine karşı çıktılar. Neyman, Fisher’in bazı çalışmalarını metamatiksel açıdan “kötüden de beter” olarak tanımlarken, Fisher da Neyman’ın yaklaşımını “çocukça” ve “Batı’daki entellektüel özgürlük adına korkunç” olarak nitelendirdi. Bu kavga, istatistikçi olmayan klinisyenlerin her iki konsepti birbirine yaklaştırıp beraber kullanarak yazdıkları kitaplar ve uygulamalar sayesinde bir karışık sisteme dönüştü. Tamamen bir kabul olarak başlayan sıfır hipotezinin %5 ihtimalle rastlantısal olarak elenmesi ihtimali birden farkın anlamlılığı kavramına dönüşerek en azından istatistikçi olmayan klinisyenler için anlaşılması ve içinden çıkılması imkansız bir hale geldi.
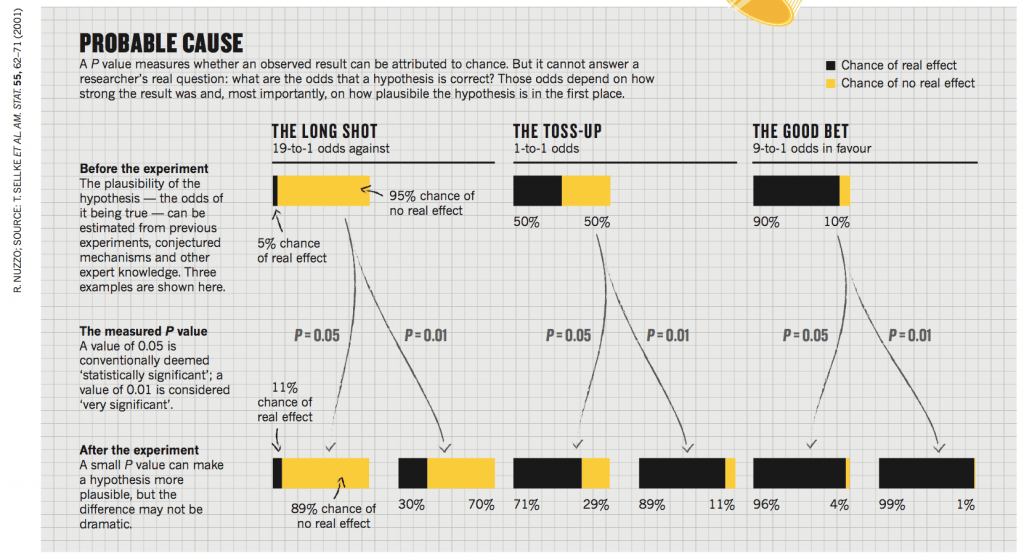
P değeri, gözlenen sonucun ne düzeyde rastlantısal şansa bağlanabileceğini gösteren ihtimal olarak tanımlanıp, aradaki farkın anlamlılığına doğru evrilince bu hatayı daha net belirtmek için “Muhtemel Sebep” kavramı (probable cause) ortaya çıktı. Çünkü, P değeri araştırmacının esas aklındaki sorunun yanıtını vermekten çok uzaktı. O soru ise hipotezimin doğru olma ihtimali nedir sorusudur. Ancak bu noktada çok önemli bir basamak hep atlanır. O da hipotezin daha çalışma yapılmadan önce ne derece ihtimal dahilinde olduğudur. Örneğin, %5 ihtimalle doğru olabilecek ekstrem bir hipotezi test eden bir çalışma yapıyorsanız, p değeriniz 0,05 düzeyinde “istatistiksel olarak anlamlı” fark gösterse bile hipotezinizin gerçek hayatta doğru olması ve farkın gerçek olma olasılığı sadece %11’dir. Bu muhtemel sebep kavramına ilerdeki yazılarda tekrar değineceğiz.
Sonuç
Sonuç olarak, p değeri hepimizin içine işlemiş olan “anlam” kelimesinin karşılığı kesinlikle değildir. Amacı, hedefi farklı olan bir konsept olarak son derece yanlış ifadelerle kullanmaya devam etmekteyiz. Bir faydanın ya da bir farkın ne kadar olduğu sorusuna yanıt vermez, sadece şansa bağlı olarak o sonuçla karşılaşma ihtimalimizin bir göstergesidir. P değeri yerine %95 güven aralıklarını, Odds ve Likelihood Ratio’ları kullanacağınız günler umarım ki bu yazıdan sonra daha yakın olsun.
Referanslar
- Doll, H. (2005). Statistical approaches to uncertainty: p values and confidence intervals unpacked. Evidence-Based Medicine, 10(5), pp.133-134.
- Sedgwick, P. (2012). What is a P value?. BMJ, 345(nov21 1), pp.e7767-e7767.
- Sedgwick, P. (2010). P values. BMJ, 340(apr28 1), pp.c2203-c2203.
- Nuzzo, R. (2014). Scientific method: Statistical errors. Nature, 506(7487), pp.150-152.